Plan2Explore

The P2E algorithm

In DreamerV1 [2] we saw that the world model is reilably learned by the world model. In [1] an ad hoc method is proposed to learn the world model by exploring the environment and to increase the generalization of the world model, so that different tasks can be learned with less effort.

The main idea is to replace the reward of the task with an intrinsic reward that estimates the level of novelty of a state of the environment. The newer the state, the more intrinsic reward is given to the agent. If the model vistis always the same state, the intrinsic reward will be low, so the agent is pushed to visit states it has never encountered before.

The ensembles and the intrinsic rewards

Now the question that arises is, how does one compute the novelty of a state? Sekar et al. introduced the ensembles (Figure 1), i.e., several MLPs initialized with different weights, that try to predict the embedding of the next observations (provided by the environment and embedded by the encoder). The more similar the predictions of the ensembles are, the lower the novelty of the state. Indeed, novelty comes from the disagreement of the ensembles, and the models will converge towards more similar predictions for states that are visited many times.

Figure 1: How the ensemble works. [1]. The ensemble is an MLP that tries to predict the embedding of the next observation. Several ensembles are exploited to compute the novelty of a state: the greater the disagreement between them, the newer the state. It is possible to notice from this picture that the stochastic state is the one computed by the transition model.

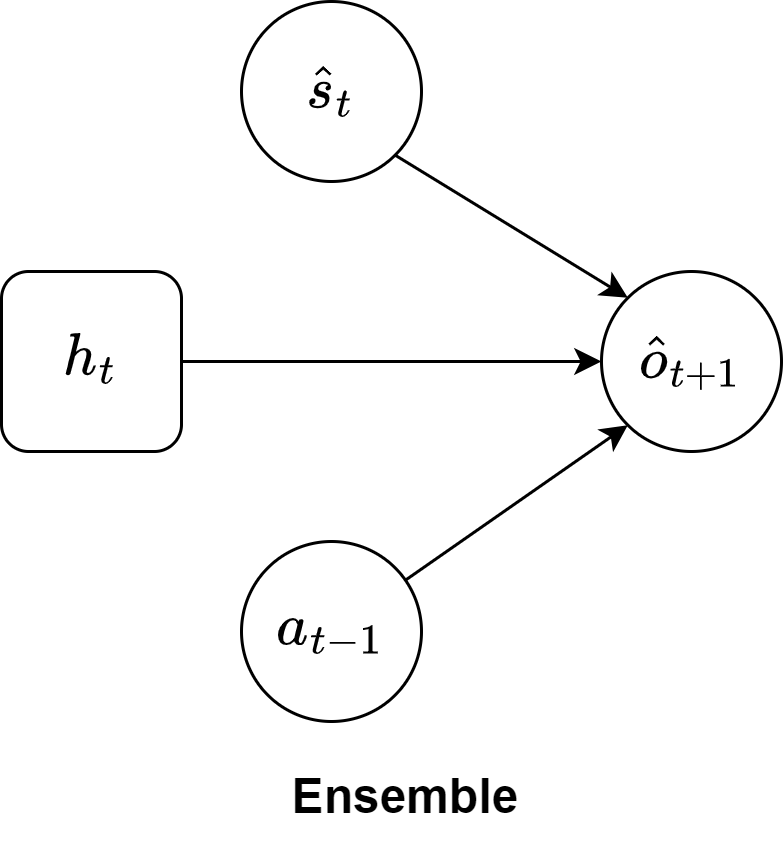
A note should be made about the prediction of the embedding of the next observation: the ensemble takes as input the latent state, composed by the predicted stochastic state (computed by the transition model) and the recurrent state, and the performed action (the one that led to the latent state in input). It is necessary to use the stochastic state predicted by the transition model because during the imagination, the agent has no observations, so the ensembles must be trained on the same kind of data.

Now we need to measure the level of disagreement between the ensembles: in the solution proposed in [1], the disagreement is given by the intrinsic reward ($\text{ir}$), i.e., the variance of the outputs of the ensembles.

Where $K$ is the number of ensembles, $\mu_{k}(s_t, h_t, a_{t-1})$ is the output of the $k$-th ensemble at time step $t$, and $\mu^\prime = \frac{1}{K} \sum_{k} \mu_{k}(s_t, h_t, a_{t-1})$ is the mean of the outputs of the ensembles. These intrinsic rewards are computed at each gradient step during the imagination phase.

Zero-shot vs Few-shot

With the world model trained to explore the environment, one can test:

• in a zero-shot setting whether the exploration experience is useful to learn the task at hand: given the task rewards (the ones that the environment returns at every step and that represent the tasked to be solved) obtained during the exploration, is the agent able to learn a behaviour that also solves the task?
• in few-shot setting whether finetuning the agent with few interactions with the environment (150k steps tipically) helps to improve the performances further. In this setting the agent will collect new experiences with the intent to maximize its performance in solving the task: it is no more interested in exploring the environment.

Both settings can be tested on different environments than the one explored to assess further the generaliztion capabilities of the agent.

Experiments

We have conducted some experiments on the CarRacing environment to assess the generalization capabilities of P2E. The results are shown in Figure 2 and Figure 3.

Check out our implementation.

References